精密压力表是应用广泛的压力标准计量仪表之 一，在使用过程中，尤其在建立计量标准时，经常需要 进行误差分析。本文就其各项误差对测量总不确定度 的影响进行分析，并以0.4级精密压力表为例计算总不 确定度。精密压力表的误差来源，主要有仪器设备、人 员、环境条件、使用方法等。

1、仪器设备误差

上级标准器的极限误差。精密压力表的量值是 由二等标准活塞式压力计传递的，其极限误差为 0.05%。以5 i表示该项误差，则有：5 i< 0.05%

精密压力表的基本误差。精密压力表被检定时 的基本误差包括：示值误差、来回差和轻敲位移。

示值误差：理论上讲该项误差可以参照检定证书 上数据进行部分修正，但是实际工作中几乎没有人进 行修正，所以仍应将它视为一个不确定分量。以5 a表 示该项误差，以△表示压力表的允许误差的绝对值，则 有：| 5 2i| < Ac

回程误差：以5 22表示回程引起的误差，则有： | 5 22I < A。

轻敲位移：以5 23表示轻敲位移引起的误差，则

有：| 5 2s| < A/2。

2、人员误差

精密压力表的人员误差是指使用或检定时读数不 确定所产生的误差，_般以分度值的1/10估算。0.4级 压力表最少分格数为80倍，对应的估读误差为： | 5 3| < 0.125%。

3、环境误差

由于弹性元件的弹性系数与温度有关，精密压力 表的使用温度和检定温度不同将造成温度附加误差。 该项误差不易修正，也应作为一个不确定度分量。精密 压力表的使用温度通常为20± 5°C,其温度系数大于 0.04%/ °C,其最大温度附加误差为：| 5 J < 0.2%。

4、方法误差

指压力表的安装姿态和安装位置，对测量结果的 准确性有很大影响，但该项误差可以通过正确的安装 和使用来消除，因此将方法误差忽略不计(5 5=0)。

5、精密压力表的基本误差

以上七项误差如果是相互独立的，只要将它们分 别换算为标准不确定度，再用均方根法就可以计算出合成标准不确定度。但是，精密压力表的示值误差、来 回差和轻敲位移是相关的，其取值相互约束，因此不能 用来直接计算合成不确定度。以下分别讨论三种最不 利情况下三项误差对总不确定的影响。

(1)示值误差达到最大正值，来回差为最大值时， 若轻敲位移也取最大值，如图1所示，在回程时轻敲位 移只允许从下往上移动。此时压力表示值的误差分布 范围-A/2〜A,不确定度为0.75A。

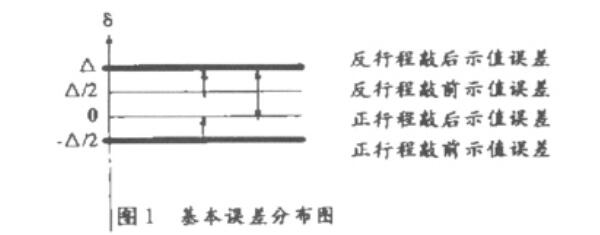
反行桩敲后示值供爰 反行《敲前示值成農 正行《敲后*值*4 正行《敲«示值*羞

-A/2

H9 1 基本设羞分布《

{2}示值误差达到最大负值，来回差为最大值时， 若轻敲位移也取最大值，如图2所示，在正行程时轻敲 位移只允许从上往下移动。 此时压力表示值误差的分 布范围为-A〜A/2,不确定度为0.75A。

反杆《敲旖*值*差 反行《敲后示後谈羞 疋行《敲旖示值供裊 £衿《敲£示值供篪

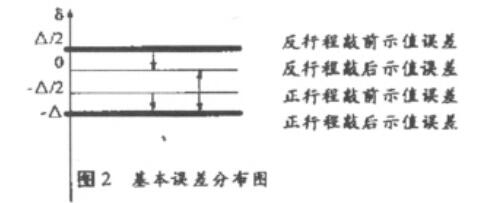
田2基本4羞分布》

(3)示值误差在行程时为-A/2,在反行程时为 A/2,来回差为最大值，此时轻敲位移可以在任意方向 达到最大值。如图3所示，

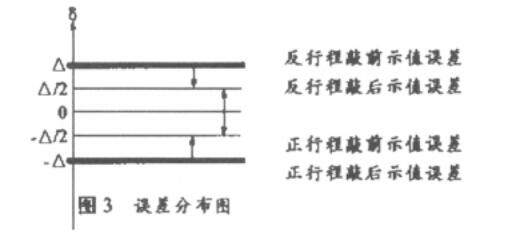
此时压力表示值的误差分布 范围为-A〜A,不确定度为A。

以上是精密压力表不确定度能够达到最大的三种 极限情况，其中第三种不确定度最大，其值A。即：在示 值误差、来回差和轻敲位移的综合作用下精密压力表 的不确定度不大于A,置信因子为3。

6、合成不确定度的计算

由上级标准器引起的不确定度^^=0.05% (k= 3)； 由基本误差引起的标准不确定度：U=0.4%(k=3)油人 员估读误差引起的不确定度XJ3=0.12%(k=3)；由环境温度引起的不确定度U=0.2%(k=3

以上四项不确定度分量相互独立，故合成不确定 度为：U= VUj2+U22+U32 =0.47% (k= 3)

精密压力表的示值误差、来回差和轻敲位移三个参数是相关的，因此不能用均方根法直接计算合成不确定度，而必须将三个量综合考虑。对0.4级的精密压 力表，在20± 5°C条件下使用时，其不确定度为0.47% (k=3),其它等级的压力表可以用相同的方法计算。