详细论述了千斤顶与压力表校验张拉力与表值回归分析法。

规范规定，预应力混凝土用千斤顶与压力表的 定期检测时，两者应视为一个单元，同时校验，配套 校验，其目的为确定千斤顶张拉力（kN)与压力表读 数（MPa)之间的关系曲线。校验单位用标准测力仪 对千斤顶进行力值校验，得出压力表读数值（以下 简称表值）和与其对应的标准测力仪显示值（下简 称力值）。以某顶号为2013，表号为7707的校验数 据为例，进行回归分析，以揭示由实验检测结果反映 物理量力值与表值之间关系的内在规律，并找出它 们之间的定量表达式-回归方程。

1.回归分析

实验已证明，千斤顶拉力值与压力表读数值之 间回归关系是一元线性回归，也可以从散点图观察 得知。我们根据表1的数据，找出千斤顶拉力（设 为y)和表值(设为x)两个变量间的经验公式：

y = b +ax (1)

(1)式就叫做y对x的回归线（也就是回归方程)

由于建立两个变量间直线关系的方法有多种， 所以不同人，用不同方法，所得到的系数a、b可能不 同。下面介绍建立两个变量y、x之间直线关系式的 几种常用方法，供大家参考和比较使用。

(1)作图法:以表1值为例 在坐标纸上作图，以横坐标代表表值，以纵坐标 代表力值，将表1中10对测试值绘于图，可得10个 点，通过10点划过一直线使两边分布均匀，这条直 线表示y = b + ax，就是力值与表值的相关式，延长

直线使之与纵坐标y轴相交，这个交点至零点（坐标 原点）的距离即为截距b值，直线与x轴交角a的 正切，即为斜率，斜率a = tgx =Ay/Ax。以表1值求 a值，可以量取图上Ay、Ax长度，也可量a角，也可 选任意两点计算，如表1的第2和第8组计算： a=Ay/Ax= (821. 8 - 126. 4) /(42 - 6) =695. 4/36 =19. 32

b =0(第 1 组 x = 0，y =0) 这时力值与表值的关系式 y =b +19. 32x (2)

值得注意的是用作图法求两个变量之间直线经 验公式时，特别要注意b与a的正负号，当因变量y 随自变量x增大而增大，或随x值减小而减小时则 斜率为正号，反之为负值，其相关系数Y可用后面 将介绍的简易近似法求得，本例：丫 = - cos(10/10) n =1

（2）选点法

先将力值与表值重新按大小次序排列（本例已 按大小顺序排列），在10对测试值中大小向两端任 选一对测试值，建联立方程: y1 =b + ax[ y2 =b + ax,

如选第2对和第8对测试值，解联立方程 126. 4 =b +a >6 821. 6 =b +a X42 求得 b =1. 05 a = 19. 3166

则相关关系式为：y = 1. 05+19. 3116x (3)

（3）平均法

把各组值按大小排列，再分成前5对为一组，后 5对为另一组，求出两组测试值x和y的算术平均 值，x和y。

第 1 组 X1 =60. 1 yi =1190. 1

第 2组 X2 =208. 0 =4067. 8

解联立方程1190. 1 =b +60a

4067. 8 = b +208a

得 a = 19. 443, b =2. 36

就可得出直线关系式：y=2 36 +19. 443x (4)

(4)最小二乘法

最小二乘法原理是使各测得值与统计所得到的 关系直线间的误差平方和为最小,这是一种常用的 统计方法。

计算结果a = 19. 426, b =5. 15,相关关系式为y =5. 15 +19. 426x (5)

上述4种求直线方程的方法都可应用，比较4 种方法得出的关系式可以看出，b值相差多,而a值 相近,所以相差不是很大,下面任选几组值代入进行 粗略检验,如选第6组实测值：

以 x = 30代入(2)y =0 +19. 32 X30 =579. 6,其 与实验‘真值” = 589. 3,误差为1. 6%。

以 x = 30代入（3)得出 y = 1. 05+19. 3116 X30 = 580. 5,其与实验真值”y =589. 3,误差为1. 5%。

以 x = 30代入（4)得出 y=2. 36 + 19. 44 X30 = 585. 6,其与实验真值”y = 589. 3,误差为0. 6%。

以 x = 30代入（5)得出 y=5. 15 + 19. 426 X30 = 587. 8,其与实验“真值” y = 589. 3,误差为 0. 25%。

由于这4种方法求得的相关系数都近似于1。 利用表1数据不用求相关回归方程,直接内插更为 方便准确,这也是规范不要求必须求回归方程,而检 测单元也提示“对所需要的负荷点,可通过内插法 求得的原因。

2.线性回归方程的效果检验

(1)相关系数检验:在实际工作中,只有当x和 y之间存在某种线性关系,所配出的直线才有意义。 检验回归线有无意义。数学上引进相关系数T这 个量，Y的绝对值越接近1, x与y的线性关系越好， 如果T接近于0,则认为x与y之间没有线性关系， 但不排除x与y之间有非线性关系，T的正负号取 决于回归线斜率a的符号,对所分析的自变量x和 因变量y,只有当相关系数Y的绝对值大于一定程 度,才可能用回归线来表示他们之间的关系,这要通 过‘相关系数检验表”检验,表中数叫做相关系数起 码值,只有求出相关系数大于表中数,才能考虑用直 线来表述x与y的关系，‘相关系数检验表”一般数 理统计书中都有,今摘录如表2。

可以看出测试的组越多,起码值越小,某标千斤 顶与压力表值得相关系数Y远大于表2的起码值 0. 632和0. 765,说明直线关系数非常明显、密切,这 也是检测单元说明中不用求回归方程,可直接用内 插法求解的依据。

(2)回归方程效果检验

前面已述，回归方程在一定程度上反映两个量 之间的内在规律,但在求出回归方程后,如何利用 它,根据自变量x的取值来控制因变量y的取值,以 及控制精度如何等,都是我们所要关心的。确定a、 b的数值后建立了方程，yt =b + ax；从公式中知道对 每个给定的自变量&值就有两个y；值,即实测值y； 和推定值（或称预测值、估计值）y;',他们之间误差 A =y； -y；。(上面几种回归分析,我们已举例算出 代表点的误差）所以有必要进行线性回归方程的效 果检验。数理统计理论已证明标准差愈小，回归方 程预报的值愈精确(按正态分布有95. 4%的y值落 在y=b ±2s + ax之间，本例样本标准差Sx = 1. 784)。

综上所述,通过回归分析、相关系数的显著性检 验和回归方程的检验,可知实测数据与回归方程的 相关密切程度,主要由相关系数T来判断，T愈接近 于1,说明相关愈密切。对回归方程所揭示的规律 性是否明显,以标准差s来表示,s愈小,说明回归方 程预报越精确,反之亦然。

应该指出,在实际问题中,有时自变量和因变量 之间不一定是线性关系,而可能是某种非线性关系， 这类非线性问题可以通过变量变换,转化为线性回 归模型来解决,本例千斤顶拉力和压力表值关系用 一元回归分析计算,这只是线性回归中最简单的情 况,在绝大多数实际问题中,影响因变量的因素往往 不止一个,而是多个,这就需要用多元回归分析来解 决,而多元回归分析原理与一元回归分析基本相同， 只是计算上复杂一点，实际操作上,二元回归问题， 只要借用简单计算器就可以轻易地建立二元回归方 程，y = a+b?x +cx；,同时求得复相关系数R。

3.相关系数简易、近似求法

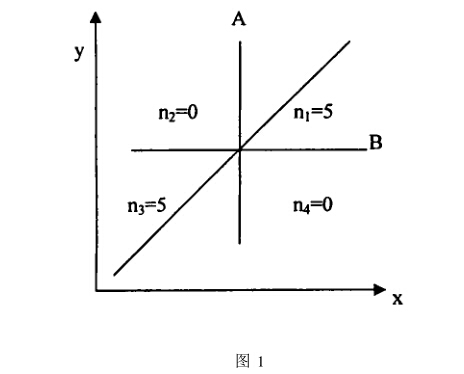
将U,y;)多组值在平面上作图（图1),作垂线 A将点子左右均分,再作水平线B将点子上下均分，

尽量使A、B线上无点,若右上,左上、左下、右下点 数分别为 n ,巧，巧，nt,则 了 = - cos[ (n +n,) / S n ] n。

本例 n =5, n, =n, =0, n, =5 Y = - cos[ (n + n,) /6n]n = - cos[ (5 + 5) /

10]宂=1

至于因为相关系数T小于某个值如0. 9999应 进行“单点值标定”要弄清这个要求是否有必要， 本人认为应首先弄清以下几点：

（1）何为“单点值标定”单点值是否理解为因 为检定时标准测力仪显示值与压力表读数值,线性 回归，T不符合要求,就采用视需要的各张拉值,确 定对应的表标值做梁张拉时控制的依据,这种做法 实际上是说校准检验时，x、y回归上存在大的误差， 使得相关系数T不符合要求,实际上回归分析对不 同点数n,有不同检验起码值要求。例如:只有3个 点，P = 1时T =0. 9999也是不符合直线回归条件 的。单点标定必须保证误差不能出现在单点值上， 这种做法等于放弃保证率可达95%以上数理统计 法,而采用保证率只有50%单点计算法。

（2）“单点值标定”在梁片张拉时的适用性 单片梁张拉至少要单点标定10% (Tk、20% (Tk和100% ^k三个点,而一个制梁场梁片有多种,就得每 一种梁都在这个千斤顶、压力表上有三个校准值,这 些孤立点间是否也要有建立相关系数的必要？

（3）标定时,标准测力仪显示值准确到百分位, 压力表读数值为整数位,也就是说表值保留有一位 可疑数字,即有±1个单位（MPa)误差。

我们试做以下计算,将最小二乘法得到的回归 方程y = 5. 15 +19. 426x,用y的计算值y=587. 8代 入求x = 29. 9933MPa,而单点x真值x = 30,误差A =30 - 29. 9933 =0. 0067 (MPa),这与检定表值误差 0. 5MPa相差两个数量级,而且0. 0067MPa这个值 在压力表上根本反应不出来(表刻度值为1MPa)。