针对基于机器视觉的指针式压力表校验系统，给出了一种采用帧差分法和角度法自动识别指针仪表读数的 方案，并且为了解决残缺指针区域的质心偏移问题提出了一种利用区域极值点确定指针质心的方法。首先基于霍 夫圆检测进行表盘中心定位和表盘分割；然后采用三帧差分法检测指针区域，并从其八方向极值点中选择最接近指 针区域最小外接矩形对角顶点的两点来定位指针质心；最后连接指针质心和表盘中心以计算指针偏转角度和识别 读数。实验结果表明基于区域极值点的指针质心定位可以简单有效地修正残缺指针区域质心偏移，整体方案能够 较准确地识别指针式压力表读数。

1.引言

指针式模拟仪表仍然以其低成本和高可靠性等优势占尽管数字化和智能化是仪表行业发展的主流趋势，据一定市场。但是在对指针仪表进行出厂前检验和周期性校验时，传统的人工方式效率低下，而且劳动力成 本的日益提高也增加了生产经营压力。然而随着计算 机和摄像设备性能的提升和价格的降低，基于机器视觉 技术对仪表进行自动校验变得可行且有效' 所以作为 影响整体检验和校验性能的核心技术，指针仪表读数自 动识别受到了很多关注。本文面向实际需求设计了 一套用机器视觉方法对某指针式气体密度继电器的压 力示数进行自动识别的方案。

指针仪表读数识别的关键在于指针检测，现有的方 法包括直线拟合法M、帧差法、Hough直线检测法、 中心投影法、表盘图像特征法以及对这些方法的综 合。本方案所面向的仪表指针较短而且不直接与表盘 中心相连，因此直线拟合方法并不适用。而在本文所针 对的实际校验系统中，每个仪表都要经过10个不同压 力值的测试，每测试一个压力值校验平台就捕捉一帧对 应该数值的仪表监控图像，这样一个仪表对应着10幅 背景相同但是指针偏转不同的图像。因此本方案采用 了一种帧间求差方法，即基于前后帧差分检测指针区域 并提取其质心，然后将质心与表盘中心连线以确定指针 偏转角度，从而使用角度法识别读数。在基于帧差法 进行指针检测时，如果指针与表盘刻度线有重叠，检测 到的指针区域会出现残缺，按照传统方法提取到的质心 会存在偏差。为了解决这个问题，本文提出了一种利用 指针区域八方向极值点寻找质心的简单方法，该方法既 可以修正指针质心偏移又能避免对残缺指针区域进行 修复性拟合。

2.系统整体方案

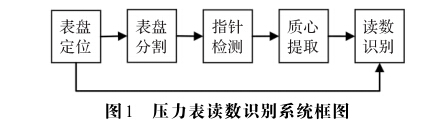
如图1所示，整体读数识别方案包括表盘定位、表 盘分割、指针检测、质心提取和读数识别5个主要组成 部分。

表盘定位：基于Hough圆检测用第一个测试 值对应帧来定位表盘圆环中心点和刻度线中间校准点。

表盘分割：以检测到的表盘中心为圆心，根据表 盘尺寸比例从测试值对应帧中切割出适合指针检测的 环形区域。

指针检测：采用三帧差法进行指针检测，得 到包含测试值所对应指针区域的二值图像。

质心提取:对包含指针区域的二值图像做连通 区域检测，获取指针区域的极值点并计算其质心。

读数识别:先连接表盘中心点和刻度线中间校 准点得到刻度基准线，然后将测试值对应的指针质心和表盘中心进行连接，根据连线与基准线的夹角识别读数。

3.表盘定位和分割

3.1表盘定位

虽然自动校验平台有固定仪表的装置，但是不能保 证每个被测仪表的位置完全相同，所以需要对表盘进行 定位以提高精度。在对每个仪表进行多值测试时，只需 用第一个测试值所对应的图像进行一次初始化定位，后 续测试时可以直接使用该定位结果。如图2所示，确定 表盘位置主要依赖两个关键点:表盘中心点和刻度线的 中间校准点。校准点用于确定刻度线的中线位置，为后 续读数识别提供参照。

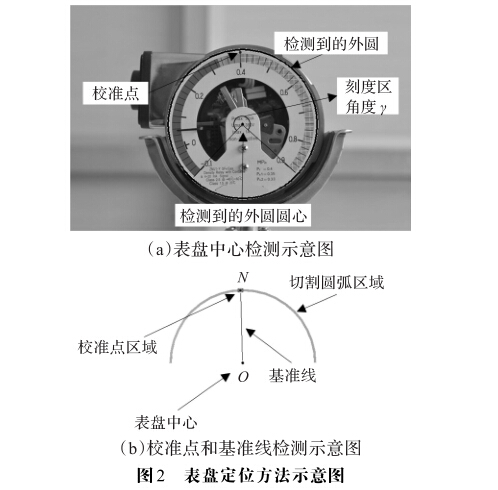
首先基于Hough变换检测圆形得到表盘外圆圆心 和半径，该圆心即为表盘中心O。根据先验知识，刻度 线中间校准点和表盘中心的距离相比于外圆半径的比 例是一定的。为了避免表盘下半部分文字的干扰，可以 利用该比例对表盘进行半圆弧切割以得到校准点所在 的上半圆弧区域。然后对切割区域进行二值化处理和 连通域检测，可以获得校准点区域信息，再通过取校准 点区域内所有点坐标的均值来定位质心N。在最终的 读数识别环节，就以表盘中心O和该校准点质心N的 连线ON (所对应的读数为0.4)作为基准参照线。

3.2 表盘分割

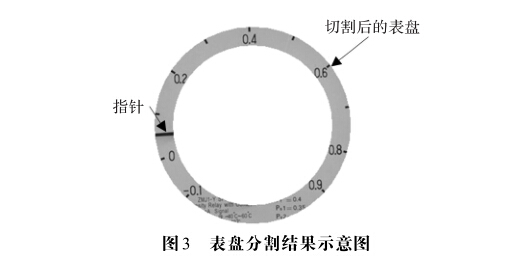
仪表表盘的中心位置有空洞而且有零件显现，在指 针转动过程中，这部分区域的变化给指针检测带来了很 大干扰。所以在检测指针之前根据表盘尺寸比例以前 面检测到的表盘中心为圆心对其进行了环形切割，只保 留适合检测的表盘区域。如图3所示，分割后的表盘背 景简单，干扰较少。这样可以避免对图像进行去噪处 理，既能提高效率又能提高系统的可靠性。

4.指针检测和质心提取

4.1指针检测

在对仪表的10个测试值对应帧进行分割提取后， 基于三帧差法用每个测试值前后两个测试值对应帧减 去当前测试值对应帧。求差操作使得无变化的背景区 域变为低像素值，而前后参考帧的指针区域本身也为黑 色(低像素值），所以在求差结果中只有当前数值对应的 指针区域变为表盘背景像素值(高像素值)。假设第n个 被测数值对应的分割后图像为In，其前后测试值对应 参考图像为1和In+1 (当n = 1时，n - 1定义为10;当 n = 10时n + 1定义为1)，前后两次求差结果分别为：

dback = In - 1 - In (1)

d forward = In + 1 - In (2)

为了提高可靠性，对两次求差所得结果进行二值化 处理并做逻辑与运算得到显示当前值指针区域的二值 化图像:

d = bw(dback) H bw(dLwaJ ( 3 )

其中bw()代表二值化处理。由于图像背景简单，本方 案选择以固定阈值进行二值化。

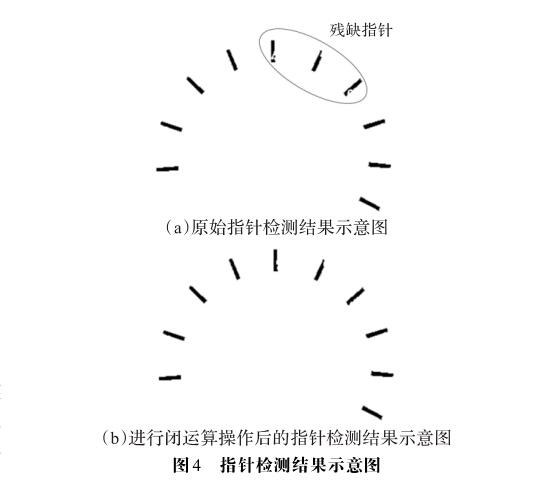
图4给出了某仪表的指针检测结果，为了方便显示 和节省空间，这里将10个检测结果对应的二值图像进 行叠加并对图像求反以保证背景为白色。可以发现，当 某个测试值对应指针落在表盘刻度线或者数字位置上 时，检测到的指针区域会留下前后参考帧的刻度线或者 数字印迹，即指针区域出现残缺。接下来采用先膨胀后 腐蚀的闭运算来初步修复残缺指针，图4(b)显示了进行 闭运算处理后的结果。

4.2质心提取

在得到代表测试值对应指针区域位置信息的二值 化图像后，可以通过连通域检测来获取区域信息，并计 算区域质心以对其进行定位。从图4可以看出，尽管闭 运算可以初步修复残缺指针，这些指针区域仍然存在缺 角或者边缘不连贯的现象。传统方法取区域内所有点 的坐标平均值来当作区域质心坐标，当指针区域出现残 缺时使用这种方法会使质心偏移而影响识别精度。最 直接的修正区域质心的方式是采用最小外接矩形或者 椭圆来包络区域，然后用外接形状的中心作为其质心。 但是这些方法需要进行多次拟合，效率不高。

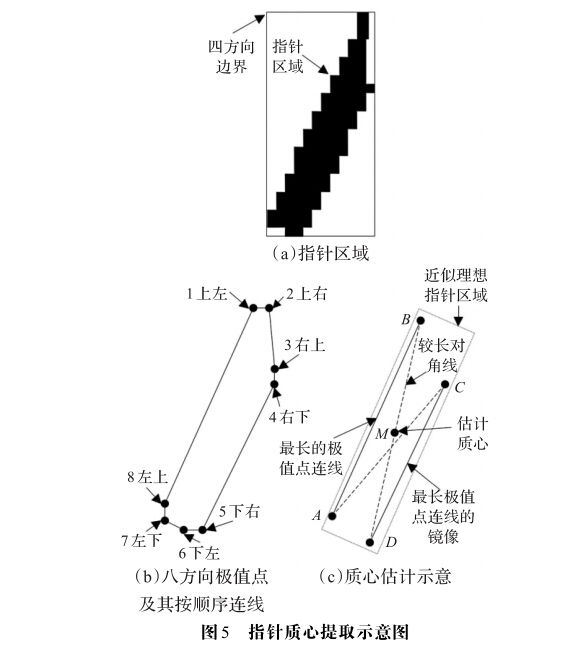
如图5所示，本文根据指针区域是近似矩形的先验 知识，从指针区域的八方向极值点中筛选最接近指针区 域最小外接矩形对角顶点的两点，然后取这两点的中点 作为质心。详细算法如下：

对指针检测结果对应二值图像进行连通域检 测，得到10个指针区域Rn，n = 1，2，...，10。

如图5(a)和图5(b)所示，在指针区域Rn内的所 有点中，寻找该区域上、下、左和右4条边界上的点。按 顺时针顺序取区域在各边界上的起点和终点组成区域 八方向极值点集合，并按上左、上右、右上、右下、下右、 下左、左下和左上的顺序排列。如果区域在某边界上的 极值点恰好只有一个，视该点为起点和终点的重合并进 行重复提取。这样保证每个区域都有8个极值点，记为 P，i = 1，2，…，8。

将各个卩免按顺时针顺序连接，得到勾勒出区域 轮廓的8条线段，两个重合极值点构成的线段长度为0。 记从第i点出发的线段为h = PiP，i = 1，2，…，8。当i <7 时，，=i + 1，当i = 8时，线段18的末端点为Pi。因此对 j的取值用下式进行转换：

j = f (i + 1) = (i + 1) mod 8 + 1{((i + 1) mod 8) == 0} x 8 (4) 其中mod代表模运算。而1{}代表指示函数：当 ((i + 1) mod 8) == 0 ”条件成立时取值为1，不成立时取 值为0。这样既能保证i = 8时j取值为1，又能防止i = 7 时j的结果被模8运算设置为0。

如图5(c)所示从所有I!中选择最长的线段lk ：

lk = PkPf (k +1) (5)

其始端点为Pk，末端点为Pf(k +1)，该线段方向是指针长 轴方向的概率最大。则最长边lk后的第4条线段为其 镜像边I\ :

厂 k = Pf Ok + 4) Pf(k + 5) (6）

其按顺序连线

图5指针质心提取示意图

最长极值点连线的 镜像

和第(3)步一样， 这里需要对k + 1、k + 4和k + 5进行公式(4)所示的转换 以保证其取值是[1，8]内的整数。如果所有l中的最长 边有多个，则取其镜像边最长的情况，如果镜像边也都 一样长则取k最小的组合。记Pk为点A，Pf(k +1)为点B，

Pf(k + 4)为点 C，Pf(k + 5)为点 D。

在最长边AB两端点和镜像边CD两端点间做 对角连线，此时较长对角连线的两端点最接近区域最小 近外接矩形的对角顶点，取这两端点的中点作为第n个 指针的估计质心Mn。

该算法通过两次筛选，在指针缺角或者有边缘凹陷 时可以获取理想指针区域的近似质心，从而起到修正作 用，而且避免了寻找区域外接形状所需的拟合操作。

5.读数识别

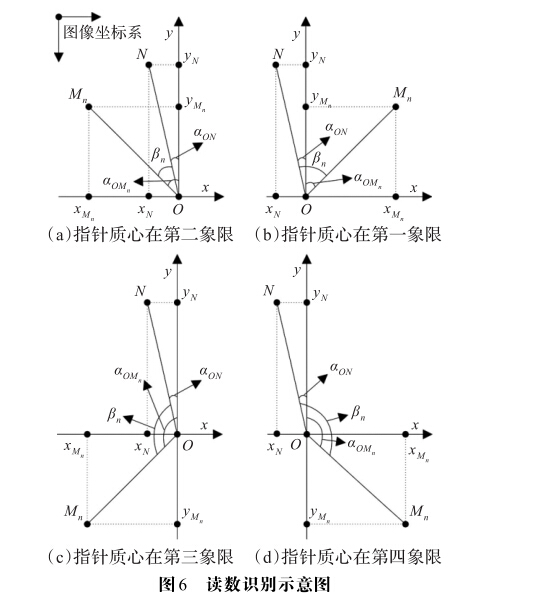
在得到指针区域的近似质心后，连接表盘中心O和 指针区域Rn的质心Mn，以OMn和3.1节中所得基准线 ON的夹角为依据来识别该指针的读数。如图6所示， 在计算夹角时将以O点为原点的直角坐标系纵轴正半 轴作为参照，分别计算ON相对于纵轴正半轴的偏转角 度和OMn相对于纵轴正半轴的偏转角度，再将两者求 差得到OMn相对于ON的偏转角度。本文统一定义偏 转角度的取值在[-n，n]之间，且逆时针偏转角度为负， 顺时针偏转角度为正。

其始端点为Pf(k + 4)，末端点为Pf(k + 5)

图像坐标系以图像左上角点为原点且坐标向右向 下递增，这与以O为原点的直角坐标系有所不同。为了 进行直观表示，这里首先对O、N和质心点Mn进行坐 标转化，假设O点的原坐标为（x。，yO)，任一 Q点原坐 标为(xe，yQ)，则Q点转换后的坐标为：

xQ = xQ -xO (7)

y Q = -(yQ- yc) (8)

经过变换，o点的坐标变为（0，0)，以o为原点的 直角坐标系中的点坐标向右向上递增。图6和后续章 节中的xN、yN、xM。和yMn分别代表变换后的N点和质

心Mn的横坐标与纵坐标。图6仅给出了 N点落在以O 为原点的直角坐标系第二象限时，指针质心Mn落在各 个象限的情况。

在仪表被固定后，其校准点N相对于纵轴正半轴 只会有小范围左右偏转，即N点落在以O为原点的直 角坐标系第一象限或第二象限，此时yN均为非负。 ON相对于纵轴正半轴的偏转角度可以定义为：

aON = arCtan(XN)，yN > 0 (9)

N在第一象限时xN为正，角度为正，ON相对于纵轴正 半轴顺时针偏转；N在第二象限时Xn为负，角度为负， ON 相对于纵轴正半轴逆时针偏转。

而指针质心Mn可能落在以O为原点的直角坐标 系的各个象限。当Mn落在第一象限或者第二象限时， 和N点一样OMn相对于纵轴正半轴的偏转角度定义为：

(aOM = arctan(xM ~M )，yM > 0 (10）

当Mn点落在第三象限时arctan(xM /yM )为正且代 表OMn与纵轴负半轴的夹角。此时OMn相对于纵轴正 半轴逆时针偏转，所以考虑到角度定义的正负将其与纵 轴正半轴的偏转角度定义为：

a3OM =-(兀-arctan(^M ~M》，xM < 0，yM < 0 (11)

n n n n n

同理，当Mn点落在第四象限时arctan(xMn为负且 其绝对值代表OMn与纵轴负半轴的夹角，则OMn相对 于纵轴正半轴的偏转角度定义为：

a4OM =兀 + arctan(xM !yM )，xM > 0，yM < 0 (12)

n n n n n

这样OMn相对于ON的偏转角度为：

Pn = aOMn - aON (13)

且OMn相对于ON逆时针偏转时角度为负，反之为正。 而ON对应的读数为0.4，整个仪表读数范围是1且图2(a) 所示的刻度区域圆弧对应的角度y为已知参数，所以 OMn对应的读数为：

vom, = 0.4 + 凡/Y (14)

6.实验结果

最后基于MATLAB对整体方案进行了实现与测 试，采集到的图像尺寸调整为531x800，圆检测时的二 值化阈值为0.5，指针检测时的二值化阈值为0.3，闭运 算处理中的膨胀和腐蚀均选用3x3大小的方形结构元 素。在质心提取阶段，还采用了区域点坐标平均法和最 小外接矩形法与本文所提出的方法进行对比。在用最 小外接矩形对指针区域进行包围时，直接使用了文献的算法，它是目前较为通用的快速寻找区域最小外接矩 形的方法。

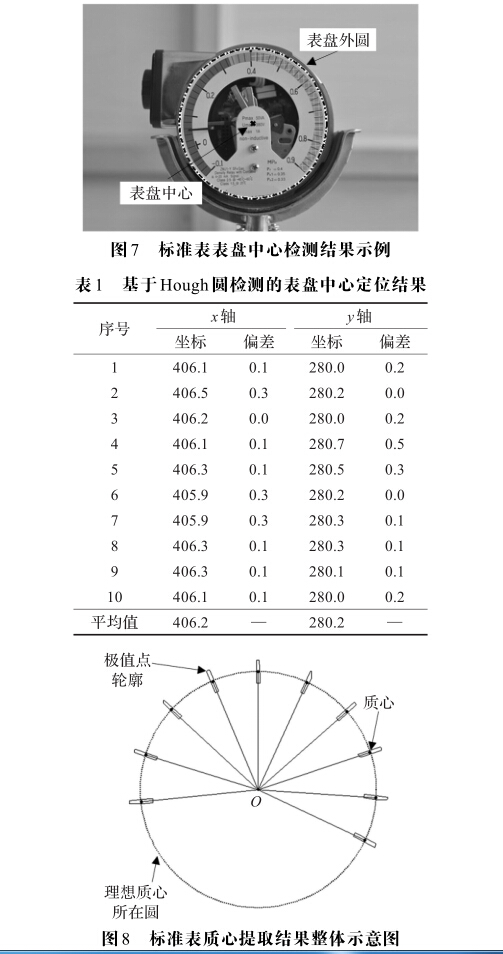
本文采用Hough变换进行表盘外圆检测和定位，后 续操作非常依赖于该检测结果。为了说明基于Hough 变换进行表盘外圆检测的有效性，图7给出了对标准表 进行检测的结果示例，图中虚线为检测到的表盘外圆。 可以看出，通过Hough圆检测能够获得理想的外圆轮 廓，这从直观上说明了采用Hough变换对表盘外圆进行 检测的有效性。为了验证其可靠性，本文对标准表的10 个测试值所对应图像都进行了检测，表1给出了每次检 测到的圆心坐标及其相对于坐标平均值的绝对偏差。 可以发现，检测到的圆心坐标在x轴上的最大绝对偏差 为0.3个像素，而在y轴上的最大绝对偏差也仅为0.5个 像素。这说明基于Hough圆检测进行表盘中心定位不 但有效而且可靠。

图8是采用本方案对标准表进行自动读数识别时 的质心提取结果整体示意图。可以看出，不管指针是否 有残缺，检测到的质心基本都在理想质心所在的圆上， 且位于区域中心。表盘中心与各指针质心的连线基本 与指针方向重合，说明了本文所提方案的有效性。

图9给出了使用不同方法提取标准表指针质心时， 较完整指针和残缺指针的质心提取结果。可以发现，在 检测到的指针相对完整时，三种方法所得质心基本重 合。而指针有残缺时，本文所提出的方法所得质心仍重 合于或接近于采用最小外接矩形法所得到的质心，而采 用区域点坐标平均法得到的质心有明显偏移。

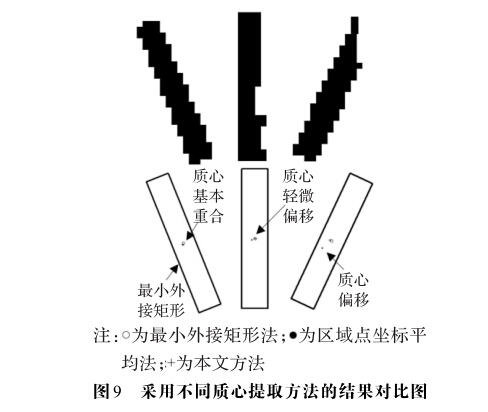
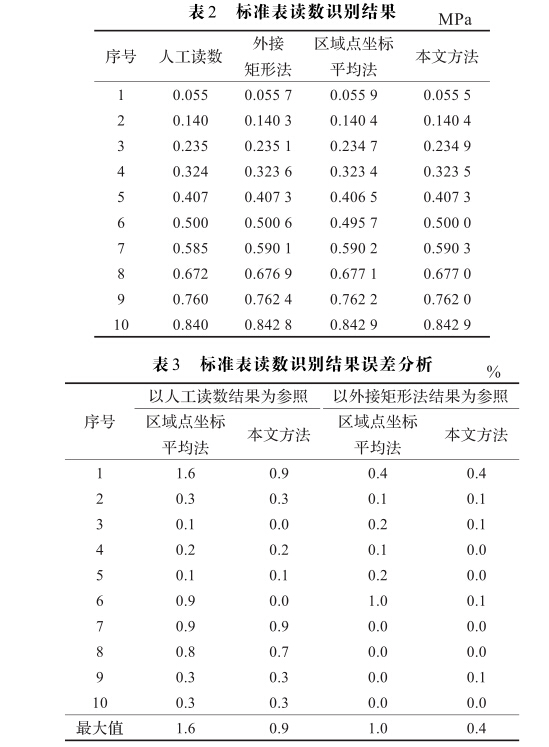
为了对各种方法进行定量比较，表2给出了采用各 种指针质心提取方法所得到的10个测试值读数识别结 果，表3给出了对应的误差分析结果。与人工读数方法 相比，采用区域点坐标平均法得到的读数识别结果的最 大相对误差为1.6%，而采用本文方法得到的读数识别 结果的最大相对误差仅为0.9%。与最小外接矩形法相 比，采用区域点坐标平均法得到的读数识别结果的最大 相对误差为1.0%，而采用本文方法得到的读数识别结 果的最大相对误差仅为0.4%。总之在指针较完整时，三种方法获得的读数基本一致;而在指针不完整时，相 比于最小外接矩形方法，区域点坐标平均法所得读数有 更大偏差。图9、表2和表3的结果说明本文所提出的基 于极值点筛选进行质心提取的方法能够有效修正质心 偏移，取得近似于最小外接矩形方法的精度。

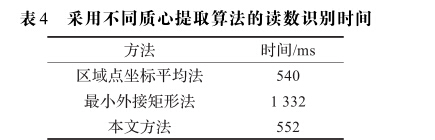
本文所提出的质心提取方法的实质是对指针区域 的八方向极值点进行两次筛选，不需要拟合区域外接形 状，理论上的时间消耗会低于最小外接矩形方法。为了

可以看出，本文所提出的质心检测方法所消耗的时 间不到最小外接矩形方法的50%，而且其时间消耗相比 于区域点坐标平均法仅有微弱增加。实验结果说明本 文所提方法能用对这些方法的效率进行对比，表4给出了用三种方法进 行质心提取时，从指针检测开始到识别出读数的时间消 耗。该时间是重复运行20次程序得到的平均结果，测 试系统配置为：ntel® Core™ 2 Duo-2.1 GHz CPU，GB 内存。

更少的时间消耗获得与最小外接矩形 方法相比拟的识别精度，这在其他采用更高分辨率图像 的应用中会更有意义。

7.结朿语

本文针对实际应用提出了一种通过对区域八方向 极值点进行筛选来提取矩形区域质心的方法，并结合帧 差法和角度法进行指针式仪表的读数识别。实验结果 表明该质心提取方法能够以较低的时间消耗有效地修 正残缺指针质心偏移，系统整体方案可以获得良好的读 数识别效果。尽管该方案针对性强，它仍能够给类似应 用带来借鉴。而且基于区域极值点的质心提取方法也 可以被应用于其他对近似矩形区域进行检测和定位的 案例。